(一) “巴塞尔协议II”操作风险计量法
在2006年的巴塞尔委员会发布的监管框架下,金融机构可以使用三种手段来计量操作风险的资本需求,分别是基本指标法(Basic Indicator Approach,简称BIA)、旧标准法(the Standardised Approach,简称TSA)与高级计量法(AMA)。简单来说,通过基本指标法与旧标准法计算资本需求,金融机构只需要将历史年度的总收入(Gross Income,简称GI)代入简单函数即可,计算方式如下:
$Capital_{BIA} =\alpha\frac{1}{n} ∑_{j=1}^3max\left\{ GI(j),0 \right\},其中 n=∑_{j=1}^3I_{GI”(j)>0},\alpha=0.15$
$Capital_{TSA} =1/3 ∑_{j=1}^3max\left\{∑_{i=1}^8\beta_iGI_i(j),0\right\}$
其中, $I(.)$代表指示函数,即如若括号中的条件成立则为1,否则为0; $GI(j)$代表银行第j年的年度总收入; $GI_i(j)$代表银行在业务条线i上的第j年的年度总收入; $\beta_i$是范围在0.12至0.18之间的参数,按照巴塞尔委员会给8个业务条线的分配来决定。此方法对量化与模型能力要求极低,一些国家的监管机构也有使用此种方式的变种来进行操作风险的计量。
在高级计量法的框架下,银行可使用内部模型来估算操作风险的资本需求,此前,金融机构须向监管机构证明其内部模型应用在《巴塞尔协议II》规定的7个事件类型内的8个业务条线中的准确性。最常用的高级计量法模型被称为“损失分布方法”(Loss Distribution Approach,简称LDA)。在损失分布方法里,通常假设金融机构有d个风险组成部分,在第j个风险组内每年的操作风险发生频数为$N_j$ 次,每次的损失用随机变量${X_{N_j}}^j$ 来表示,那么该金融机构的一年损失应为
$L=∑_{j=1}^d∑_{i=1}^{N_j}X_i^j$
金融机构的资本需求通过随机变量L的99.9%的在险价值(Value at Risk,简称VaR)来表示,即
$Capital_{LDA}=VaR_\text{99.9%}\left[ L \right]=inf\left\{l:\mathbb{P}[L>l]\leqslant \text{0.1%} \right\}$
通常,在损失分布方法里,风险发生的频数与损失数量是假设独立的。
在过去的十年里,以此三种计量方式为基础的操作风险计量法在不断发展。2014年10月和2016年3月巴塞尔委员会对操作风险资本计量方法(包含基本指标法和旧标准法)进行审查,发现在操作风险事件的数量和严重程度均大幅增加的情况下,操作风险的资本需求却始终保持稳定,甚至在旧标准法下有所下降。[6]审查表明,这主要由使用总收入作为操作风险敞口指标所致,以金融机构年度总收入来计量操作风险的风险敞口并不是一个很好的假设。
另外,因为不同金融机构所采用的数据、参数等的不同,以及金融机构之间业务的差异性,通过高级计量法计算得到的操作风险资本需求在不同金融机构之间也不具有可比性。这使得操作风险的计量成为了亟需解决的问题。
(二) “巴塞尔协议III”新标准计量法
由于操作风险先前计量方式的局限性,新计量方式的出现成为了必然。在2016年巴塞尔委员会的文件中,其删除了包括基本指标法、旧标准法与高级计量法在内的所有内容,要求未来操作风险的计量将全部采用新标准计量法。然而,在2016年文件发出不久,就有学者发表了《Discarding the AMA could become a source of op risk》,对新标准计量法提出了质疑。同时,许多金融机构发现使用2016版的新标准计量法会造成超出先前许多的资本需求。因此,巴塞尔委员会在2017年12月的最终版《巴塞尔协议III》中,将新标准计量法重新推出,对操作风险最低资本需求的算法作出了修改,建立了以业务规模为基础,利用内部损失数据进行调整的操作风险资本计量框架,旨在减少2016版算法导致的过于庞大的额外资本需求开销。
新标准计量法由下列两个核心部分所组成:
1、以依据于财务报表的BI指数(Business Indicator,也称“业务指标”)为基础计算出的业务指标因子(Business Indicator Component,简称BIC);
2、根据银行历史损失与BI指数共同计算而得到的内部损失乘数(Internal Loss Multiplier,简称ILM)。
BI指数是由三部分组成,分别为:
1、利率、租赁与红利组成部分(interest,leases and dividend component,简称ILDC),其计算方式为
$ILDC=min\left\{ | \overline{InterestIncome-InterestExpense}|,\text{2.25%}\\×\overline{InteretEarningAssets}\right\}+\overline{DividendIncome}$
其中的四个变量分别代表利息收入、利息支出、生息资产和红利收入。
2、服务组成部分(service component,简称SC),其计算方式为
$SC=max\left\{ \overline{OtherOperatingIncome},\overline{OtherOperatingExpense}\right\}\\+max\left\{ \overline{FeeIncome},\overline{FeeExpense}\right\}$
其中的四个变量分别代表其他营业收入、其他营业支出、手续费收入和手续费支出。
3、财务组成部分(financial component,简称FC),其计算方式为
$FC=|\overline{NetPnLTradingBook}|+|\overline{NetPnLBankingBook}|$
其中的两个变量分别代表交易账户净损益与银行账户净损益。
在上述三个公式中,上划线代表计算最近三年的平均值。这样,BI指数即为
$BI=ILDC+SC+FC$
而BIC是通过将BI指数与相对应的边际参数相乘而得到的。银行级别的分类与BIC的计算通过下述来完成,其中数额单位均为十亿欧元:
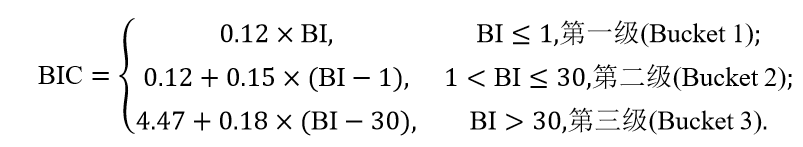
而银行的内部损失乘数的计算公式为
$ILM=ln(exp(1)-1+(\frac{LC }{BIC} )^{0.8})$
其中,损失数额(Loss Component,简称LC)等于过去十年每年操作风险损失数额总量平均数的15倍。一般而言,损失数额的计算应当使用过去十年的操作风险损失数据,但是对于数据缺失或者数据质量有一定问题的金融机构,可以使用不少于五年的历史数据。而对于没有五年内历史数据的金融机构,其操作风险资本需求应当以BIC为准。对于内部损失乘数大于1的金融机构,监管机构可以要求其以少于五年的历史数据来计算最终的资本需求。
如图1所示,在得到了BIC与内部损失乘数ILM之后,操作风险的最低资本需求应当为
$Capital_{SMA} =BIC×ILM$
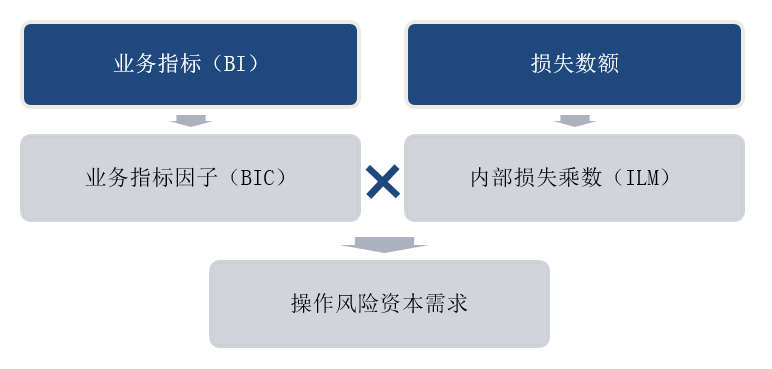
图1 SMA计算逻辑
不难发现,若金融机构的损失数额LC大于其BIC,那么内部损失乘数ILM将大于1;反之则小于1。这表明,如果金融机构的历史操作风险损失相对于其BIC更大,那么其需要持有的资本需求只有更高才能覆盖其操作风险可能带来的潜在损失。
从新标准法的计算要求可以看出,巴塞尔委员会对操作风险的理念是:操作风险会随着金融机构收入的增加而快速增大;如果金融机构在以往(十年为期)遭遇过较大的操作风险损失,则今后将更有可能出现操作风险损失。巴塞尔委员会认为原有规则计算的资本不足以覆盖某些金融机构出现的损失;因不当行为等导致金融机构损失的原因无法通过内部模型法计量。

评论