
本文基于Copula模型,以2008年美国次贷危机与2015年我国股市异常波动作为研究背景,分析了次贷危机时期(前、中、后)国外金融风险传导至我国的跨地域、跨市场路径以及2015年我国股市异常波动时期(前、中、后)的跨市场、跨产品风险传导路径。
一、次贷危机背景下跨地域、跨市场风险传染路径分析
本部分选取对全球金融市场具有较大影响力的国家(地区)—美国、欧洲、香港市场为研究对象,分析危机爆发前、中、后美国证券市场、欧洲股票市场与我国股票市场之间的风险传导路径。
首先,选取六个变量(如下表所示)分别代表不同地域的不同证券市场,计算其对数收益率序列,并拟合广义双曲分布作为边际分布,继而采用R-Vine Copula模型[1]构建风险传导分析模型。其中,基于R-Vine Copula的传导结构采用最大扩张树原理,即以各边权重绝对值之和最大化为原则进行最优化计算,所得结构能够保证整体相关性最强。映射到风险传导分析中,则表示风险能够沿该路径得到最快、最广泛的传导。
| 变量 | 代表地域、市场 |
| 恒生指数 | 中国-香港股票市场 |
| 上证综指 | 中国-大陆股票市场 |
| STOXX欧洲50指数 | 欧洲-股票市场 |
| 美银美国AA级企业债 | 美国-企业债 |
| 标准普尔500指数 | 美国-股票市场 |
| COMEX黄金 | 美国-大宗商品 |
所得风险传导路径如下图所示。其中,各连边上的字母用来标识刻画两市场相关关系的二元Copula[2]类型,各二元Copula依据对数似然估计值、AIC准则从Gumble Copula(由G代表)、Clatyon Copula(由C代表)、Frank Copula(由F代表)中选取最优模型;数字为两市场间的Kendall’s tau相关系数,数值越大代表相关性越强,风险越容易在两产品间传导。
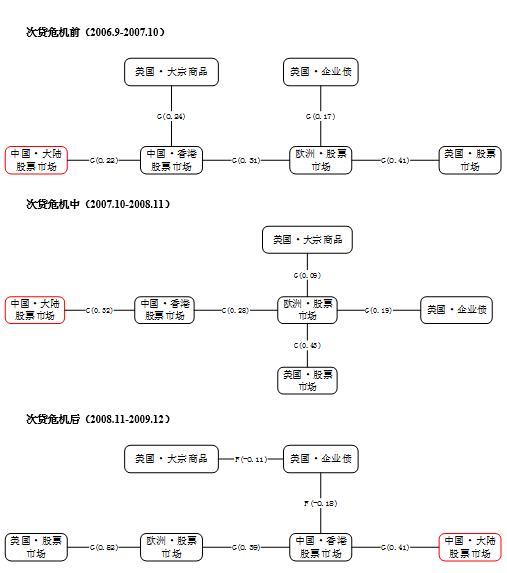
次贷危机前后跨产品风险传导图
次贷危机前,与我国大陆股票市场最为相关的为我国香港股票市场,而香港市场直接受美国商品市场与欧洲股票市场影响,欧洲股票市场又与美国股票、债券市场息息相关。因此,总结次贷危机前的风险传导路径为:美国市场金融风险通过香港市场或经由欧洲市场传导至香港市场后,对我国大陆市场造成间接传染。
次贷危机期间,与我国大陆股票市场联系最为直接的仍为香港股票市场,但与前期的不同在于美国市场对欧洲市场的风险传染效应更为强烈,并不直接影响我国市场。因此,总结次贷危机中的风险传导路径为:美国市场金融风险经由欧洲市场传导至香港市场后,对我国大陆市场造成间接传染。
次贷危机后,国外金融市场风险依然经香港市场传染至国内大陆市场,其中,美国股票市场风险经欧洲股票市场传导至香港市场,美国商品市场则经美国债券市场传导至香港市场。
二、股市异常波动背景下跨市场、跨产品风险传染路径分析
本部分主要分析2015年国内股市异常波动发生前、中、后三个阶段不同种类金融市场、金融产品间的风险传导路径。在控制模型数据规模前提下,选取十三个变量(以国内市场为主)尽可能全面的涵盖不同种类的金融市场与金融产品,如下表所示。
| 变量 | 代表市场、产品 |
| 上证综指 | 大陆股票 |
| 沪深300期货 | 国内股指期货 |
| 5年期国债期货 | 国债期货 |
| 上证国债 | 国债 |
| 美元兑在岸人民币 | 在岸汇率 |
| 美元兑离岸人民币 | 离岸汇率 |
| 恒生指数 | 香港股票 |
| Wind金融指数 | 金融股票综合 |
| WTI原油 | 石油期货 |
| COMEX黄金 | 黄金期货 |
| 10年期国债收益率 | 长期利率 |
| SHIBOR隔夜利率 | 隔夜利率 |
| 新加坡A50股指期货 | 国外股指期货 |
得出风险传导路径如下图所示。
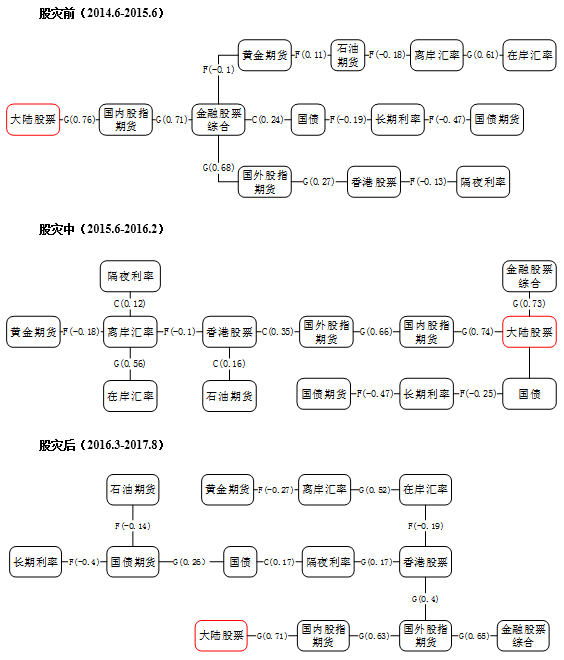
股灾前后跨产品风险传导图
总体来看,无论股市异常波动前后,与大陆股票市场风联系较为紧密均为股指期货、香港股票与国债,风险传导路径呈现为:境外股票市场→香港股票市场→境内外股指期货→大陆股票市场。另外,股指期货与股票指数之间的波动传导效应明显。相对来说,股指期货市场对现货市场的波动性影响更为强烈,股指期货的变动在短期内会引起股票指数的一个较大波动,而股票现货市场对期货市场的波动性影响力度则较为微弱。
三、结论
总结欧美金融市场对我国市场的风险传导机制如下图所示。
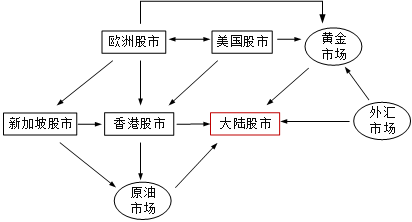 跨产品风险传导机制
跨产品风险传导机制
纵观金融危机前后,我国大陆金融市场长期受香港市场的影响;与此同时,国际大宗商品市场对我国股票市场存在直接的风险传导效应;从间接传导关系看,美国与欧洲市场持续地以大宗商品市场与香港股票市场为媒介对我国大陆股票市场产生作用。具体到各子市场,总结风险传导关系如下:
(1)国际原油市场受金融市场价格变化影响显著,而原油市场可引导我国股票市场波动,因此,国际金融市场可借助原油市场影响我国股票市场;
(2)我国债券市场较为独立,与国际债券市场分割明显,尽管如此,在极端风险状况下,国际债券市场的异动依然会传导至我国市场;
(3)国际黄金市场、外汇市场、股票市场间传导路径表现为:外汇市场→国际黄金市场→股票市场。因此,我国外汇市场风险会通过作用于国际黄金市场,进而通过黄金市场将风险传导至股票市场。
注释:
[1] Vine Copula是一种将多个二元Copula通过Vine(中文称“藤”)结构联系起来的方法,该方法可以通过一系列二元Copula的乘积迅速构建高维分布模型。常见的Vine Copula结构,包括R-Vines (regular-vines)及其两个子类别结构:C-Vines(canonical-vines)和D-Vines (drawable-vines),本文采用涵盖结构更为广泛的Regular-Vines结构。
[2] 二元Copula有众多种类,本文采用学术界常用的阿基米德Copula族中的G、C、F三种Copula模型,三者均可以计算Kendall’s tau相关系数,其中G、C还可以对收益率序列的尾部相关系数进行计算(G可以度量上尾相关性,C可以度量下尾相关性,可理解为极端情况下的相关性,比如一方行情大涨/大跌情况下与另一方产生同样变化的相关程度),F无尾部相关性意义,详细学术资料可查阅Nelsen(1999)、Embrechts(2003)或Farbrizio(2016)的专著。

评论