香农（Claude Shannon）首先将信息熵这一术语引入信息论，他在1971年的论文“能源和信息”（Energy and information）中写道：
我最关心的是该怎么称呼它。 我想称它为“信息”（information），但这个词被过度使用了，所以我决定称它为“不确定性”（uncertainty）。 当我与冯·诺伊曼（John von Neumann）讨论时，他有个更好的主意。 冯·诺伊曼告诉我，“你应该称它为熵，原因有两个。 第一，不确定性这个名称已经被用于统计学；第二，而且更重要的是，没有人知道熵（entropy）究竟是什么，所以你在辩论中总会占有优势。
熵可以用来衡量事件发生的期望的“惊讶程度”（expected surprise）。熵是信息多少的度量， 一个事件所携带的信息量跟它出现的概率反相关，一个事件出现的越频繁则每次该事件出现时携带的信息就少，反之如果一个事件非常少见，则该事件出现的时候携带的信息量就非常高。如果我们知道某件事情肯定会发生，那么我们就不会得到信息。例如扔一个所有面都是一个数的骰子，或两面一样的硬币。 在这种情况下，该随机变量的熵为0，也就是说它实际上并不是随机的。
对于一个随机变量$x$而言，它的所有可能取值的信息量的期望就称为熵。
$S = -\sum_{i} P_ilogP_i$
其中，$P_i$是事件$i$发生的概率。值得注意的是，我们不关心事件$i$的值$x_i$，只关心概率或频率。 概率和频率之间的区别很重要。 实际上我们通常不知道概率，我们只能从观察到的频率来估计概率。
熵在许多方面都很有用，尤其是量化几个随机变量哪个随机性更大。
假设我们有三个随机变量，一个是正态分布，另一个是均匀分布的，另一个是指数分布。 均匀分布的随机变量比标准正态分布的随机变量的随机性多多少？
标准正态分布随机变量的熵可以用以下R代码计算。我们不使用概率而是使用观察到的频率来估计概率。
xnum <- 10000 bnum <- 100 xnorm <- rnorm(xnum) binxnorm <- hist(xnorm, breaks= bnum) freqs_xnorm <- binxnorm$counts/sum(binxnorm$counts) log_freqs_xnorm <- log2(freqs_xnorm) log_freqs_xnorm[!is.finite(log_freqs_xnorm)] <- 0 Entropy_norm <- -sum( freqs_xnorm * log_freqs_xnorm )
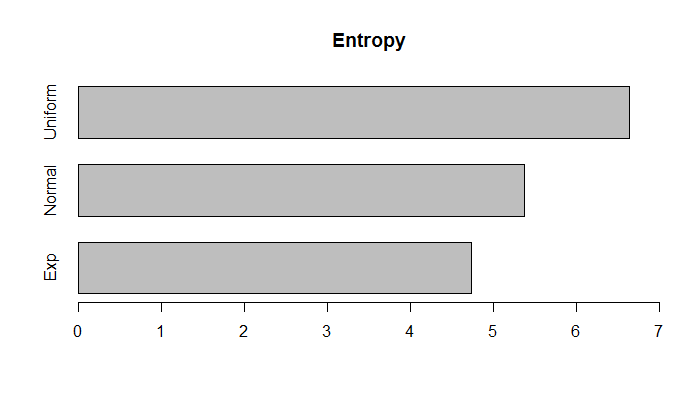正如我们所预期的，均匀分布的随机变量比正态或指数分布的随机性更大。
金融机构常见的面试问题称小球问题也可以用信息熵轻松解决。
给定$N$个小球，和一台天平，如果知道其中有一个小球偏重，但是不知道是具体哪一个，现在想用天平去把这个小球找出来，最少需要称多少次？
（1）每一次使用天平，可以得到三种可能，左偏，右偏，平衡，而且这三种可能是概率相等的，所以每一次使用天平的结果都携带$log3$的信息量。
（2）要从$N$个小球中找到那个不一样，可以有$N$种概率相同的可能，每个小球都可能偏重，这个事件所携带的信息量是$logN$。
所以最少可以称$logN/log3$次就可以指出哪一个是重的。
给定$N$个小球，和一台天平，如果知道其中有一个小球和别的不一样（不知道轻重），但是不知道是具体哪一个，现在想用天平去把这个小球找出来，最少需要称多少次？
（1）每一次使用天平，可以得到三种可能，左偏，右偏，平衡，而且这三种可能是概率相等的，所以每一次使用天平的结果都携带$log3$的信息量。
（2）要从$N$个小球中找到那个不一样，可以有$2N$种概率相同的可能，每个小球都可能偏轻或者偏重，这个事件所携带的信息量是$log2N$。
所以最少可以称$log2N/log3$次就可以指出哪一个是不一样的。
评论