经典的投资组合理论是建立在均值-方差基础上的,基本的假设是收益率服从正态分布。传统的业绩衡量指标,比如夏普比率,信息比率等,仅使用收益率分布的前两个统计矩,即均值和方差,因此对于衡量收益率不服从正态分布的情况存在缺陷。 为了克服这一局限性,研究人员提出了许多其他风险回报率:Calmar,Sortino,Sterling,Burke,Kappa等等。
2002年,Shadwick和Keating提出了一个新的业绩衡量指标,Omega比率。该指标考虑了收益率的整个分布信息,因此包括了所有高阶矩的信息。作为投资绩效主要的评级依据,Omega比率在国外已经受到业界认可。
Omega 比率定义如下:
$\Omega (r)\triangleq {\frac {\int _{{r}}^{\infty }(1-F(x))\,dx}{\int _{{-\infty }}^{r}F(x)dx}}$
其中,$r$为指定的临界收益率,$F(x)$为收益率的累计分布函数。
这个公式的分子部分是上偏矩,分母部分是下偏矩,通常我们用定积分进行计算,而阈值$r$是我们设定的临界收益率。临界收益率用来区分收益或损失,高于临界收益率的,视为收益,低于临界收益率的,视为损失,也可以称为最低要求收益率。Omega比率利用了收益率分布的所有信息,考虑了所有的高阶矩,刻画了收益率风险的所有特征。
取不同的临界收益率,可以得到关于$r$ 递减的Omega 函数。在临界收益率等于均值的时候,Omega 比率等于1。在相同的临界 收益率下,对于不同的投资选择,Omega比率值越高,投资绩效也就越好。
可以用下图来理解该指标的计算。Omega 比率就等于上方绿色面积除以下方红色面积。
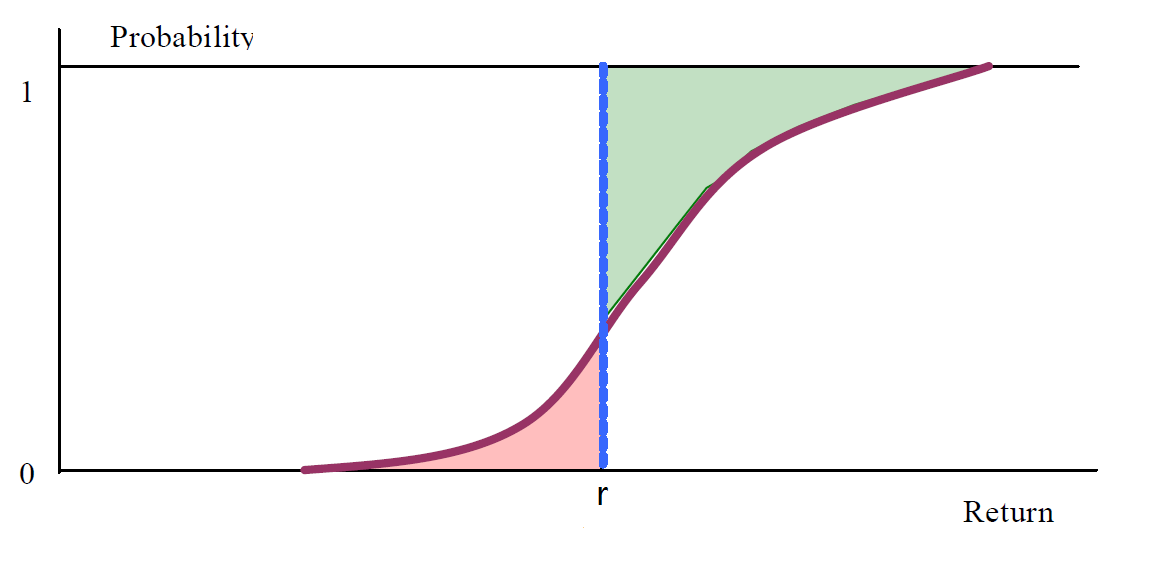
该指标也可以适合不同风险偏好的投资者。对于风险容忍度较低的投资者,可以选择较低的临界收益率,反之,可选择较高的临界收益率。
Omega比率可以转换成下面的公式:
$\Omega (r) = \frac{E[\max(x-r,0)]}{E[\max(r-x,0)]} = \frac{e^{-r_f} E[\max(x-r,0)]}{e^{-r_f} E[\max(r-x,0)]} = \frac{C(r)}{P(r)}$
其中,$C(r)$是一个欧式看涨期权的价格,$P(r)$是一个欧式看跌期权的价格,两者的执行价格都是$r$。 应用put-call parity,Omega比率也可以只用看跌期权表示:
$\Omega (r) = 1 + \frac{\mu – r}{P(r)} = 1 + \frac{\mu – r}{E[\max(r-x,0)]}$
与下面的夏普比率相比较表明,不考虑常数1,Omega比率也可以看作夏普比率变化而来,其中标准差被单侧风险度量取代,低于$r$部分的预期偏差。
$SR \triangleq \frac{\mu-r_b}{\sigma}$
我们可以得出结论,Omega比率基本上是使用一种下行风险衡量指标的风险收益比率。 实际上,它与Sortino比率非常相似:
$\text{Sortino ratio} = \frac{\mu – r}{\sqrt{E[\max(r-x,0)^2]}}$
唯一的区别是分母中的二次均值被算术平均值所代替。
值得注意的是,Omega比率并不是一个简单的统计量,而是一个带参数的函数,即$\Omega (r) $。 参数$r$是收益目标阈值(临界收益率),并定义什么被视为收益(高于阈值)和损失(低于阈值)。Omega比率的优点在于投资者偏好可以通过参数$r$集成到统计量中,与夏普利率相比,投资者可以利用Omega曲线通过改变$r$来对不同风险规避水平进行排名。
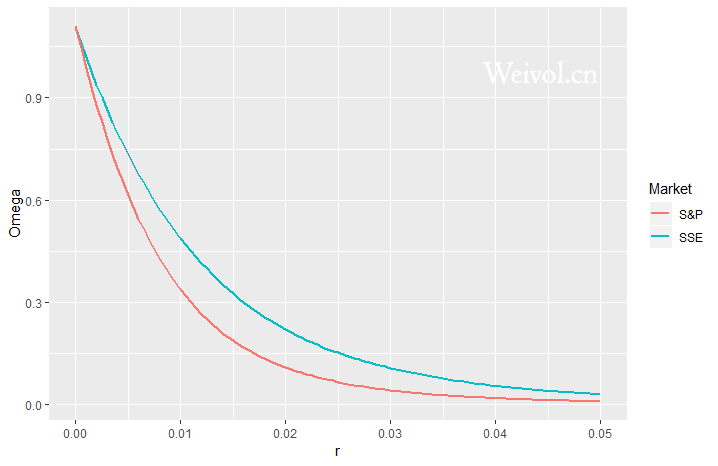
上证指数与S&P500周收益率的Omega曲线如下图:
参考:
1、Omega as a performance measure,Hossein Kazemi and Thomas Schneeweis
2、Omega比率:衡量私募基金绩效的良好指标,胡新辉

评论